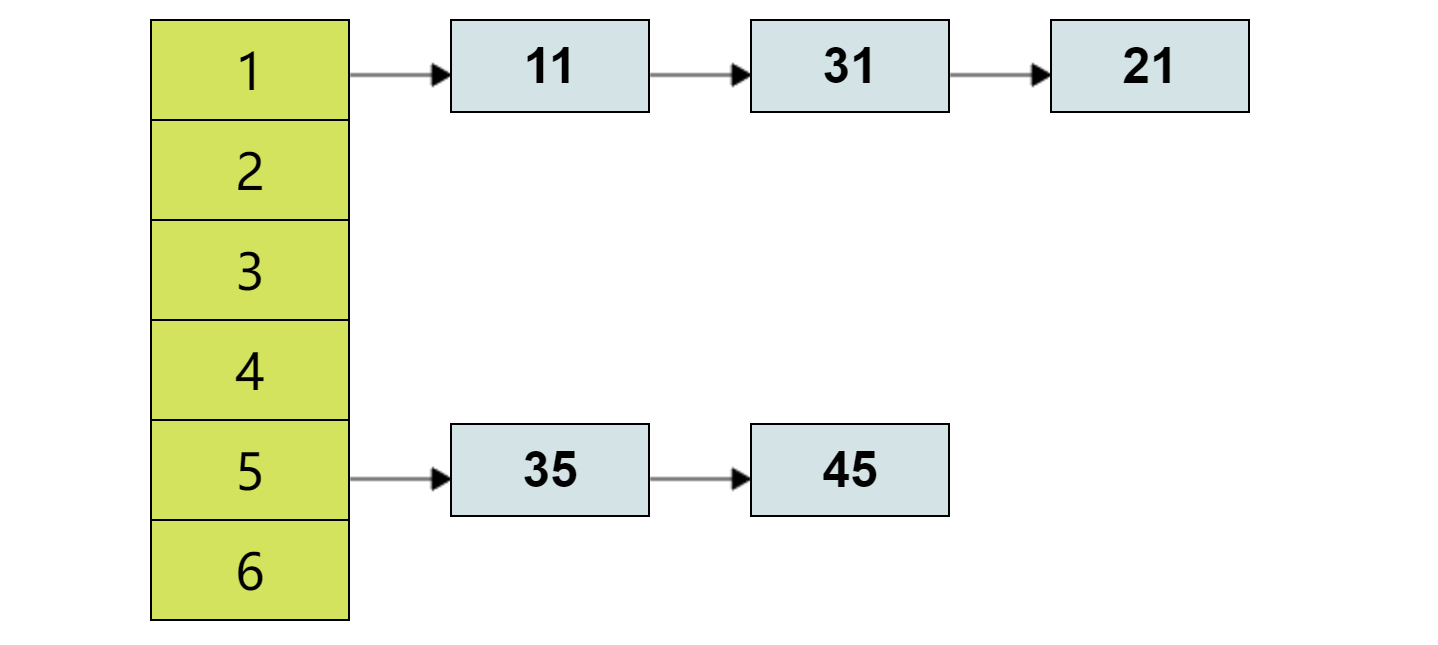
并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

1. 并查集的主要操作

  1. 初始化
    把每个点所在集合初始化为其自身。
    通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。
  2. 查找
    查找元素所在的集合，即根节点。
  3. 合并
    将两个元素所在的集合合并为一个集合。
    通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。

2. 并查集代码实现

  • 1.初始化
1
2
for(int i = 0; i < length(pre); i++)
	pre[i] = i;
  • 2.查找
1
2
3
4
5
6
int unionSearch(int root) {
	root = pre[root];//找到root的直接上级
	while(root != pre[root])//root的上级不是自己，即root不是根
		root = pre[root];
	return root;//找到根
}
  • 3.合并
1
2
3
4
5
6
void join(int x, int y){//将下x、y所在的集合合并
	int root1 = unionSearch(x);
	int root2 = unionSearch(y);
	if root1 != root2
		pre[root1] = root2;
}

3. 并查集的优化

  • 1.路径压缩

我们只需要知道某个元素是否在集合内，而无需知道这个集合的具体构成，也就是说，我们完全可以不在乎集合内部结构是否发生过变化。为了能够最快的查找到集合的根，最佳的做法就是，所有的其他元素都挂载在这个根下面，这样，只需要一次查找，就能知道根了。所以在查询的时候，对集合结构进行这样的优化

如这样的结构：

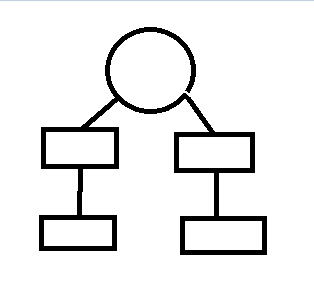
images1 —> images2

优化算法:

1
2
3
4
5
6
7
8
9
10
11
int unionSearch(int root){
	int son = root, temp;
	while(root != pre[root])
		root = pre[root]//找到了根root
	while(son != root){//如果son不是根，那么将pre[son]设为root
		temp = pre[son];
		pre[son] = root;
		son = temp;
	}
	return root;
}
  • 2.按秩合并

在合并两个集合的时候，高度较小的集合的根作为合并后的集合的根。这样的话，得到的新的集合的结构，更加接近理想的那种集合，并且新的集合的高度是不会改变的。初始时，默认只有一个元素的集合高度为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void join(int x, int y){
	int root1 = unionSearch(x);
	int root2 = unionSearch(y);
	if(root1 != root2){
		if(hight[root1] > hight[root2])//root1集合更高
			pre[root2] = root1;
		else if(hight[root1] < hight[root2])//root2集合更高
			pre[root1] = root2;
		else{//两集合一样高，默认root1做根
			hight[root1]++;
			pre[root2] = root1;
		}
	}
	return;
}