题目描述

你这个学期必须选修numCourse门课程，记为0到numCourse-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们：[0,1]

给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完    成课程 1。这是不可能的。

提示：

  1. 输入的先决条件是由 边缘列表 表示的图形，而不是 邻接矩阵 。详情请参见图的表示法。
  2. 你可以假定输入的先决条件中没有重复的边。
  3. 1 <= numCourses <= 10^5

思路

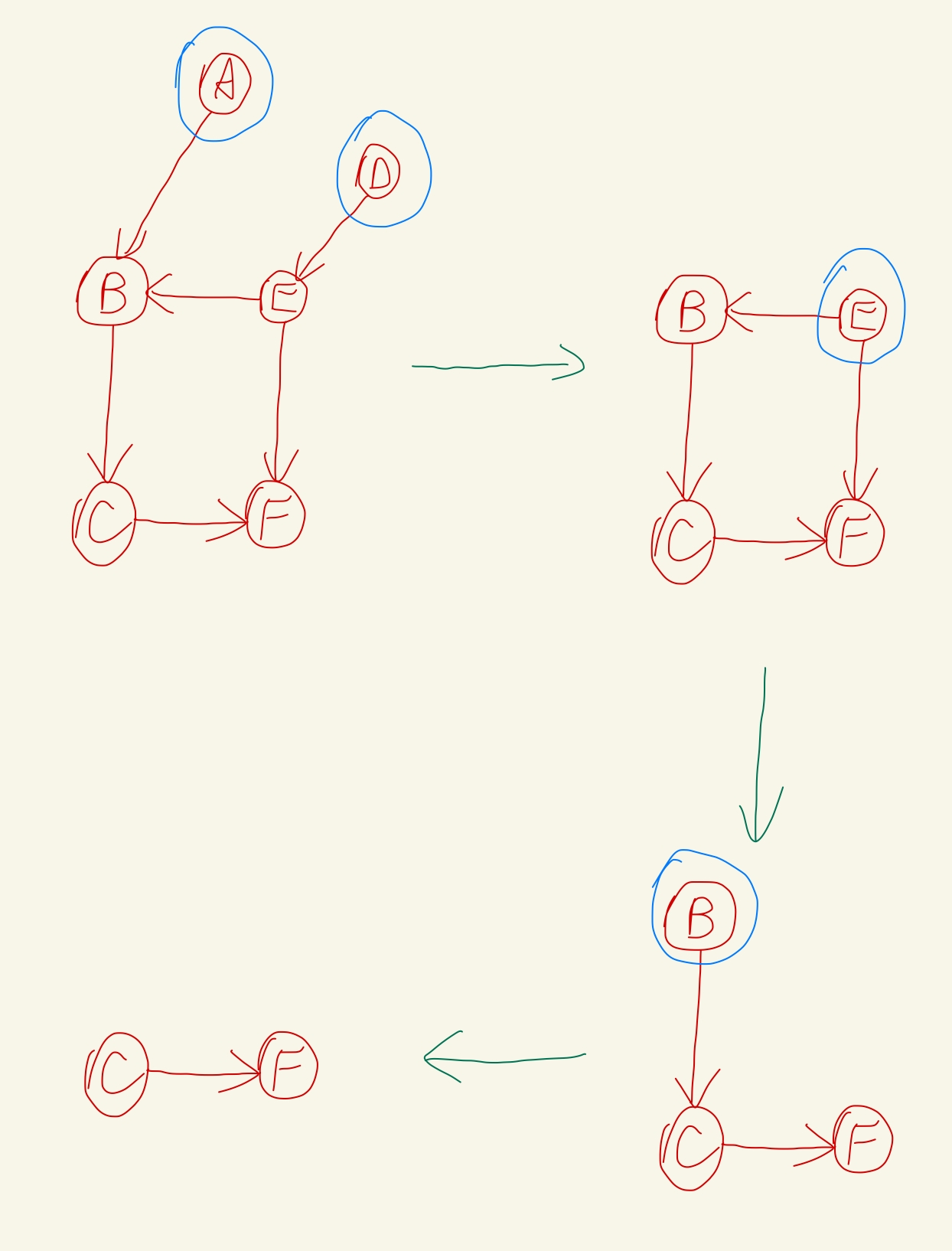
这道题实际上就是判断有向图是否存在圈（从一个节点开始，能够回到这个节点），那么在所有课程中，入度为0的课程，一定是其他课程的先修课程或者为单独的课程（既无先修课程，也无课程需要先修此课程），那么我们可以先去掉这些课程，然后将与这些课程相关联的课程的入度减一，然后再重复这个操作。如果到最后，去掉的课程数不等于所有的课程数，说明这些课程出现了圈，那么就不可能完成所有课程的学习。可以采用宽度优先搜索，遍历这些课程，即拓扑算法。

images1

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution{
public:
	bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
		vector<vector<int>> preList(numCourses);//存储能从该节点直接到达的节点
		vector<int> inDegree(numCourses, 0);//存储该节点的入度，初始为0
		for(int i=0; i<prerequisites.size(); ++i){
			int pre = prerequisites[i][0];
			int next = prerequisites[i][1];
			preList[pre].push_back(next);
			++inDegree[next];
		}
		int count = 0;//记录访问过的节点（删去的）
		queue<int> traverse;
		for(int i=0; i<numCourses; ++i){//找到最初所有入度为0的节点
			if(inDegree[i] == 0)
				traverse.push(i);
		}
		while(!traverse.empty()){
			int cur = traverse.front(); traverse.pop();
			++count;
			for(int i=0; i<preList[cur].size(); ++i){
				if(--inDegree[preList[cur][i]] == 0)//减去一个入度以后，入度为0
					traverse.push(preList[cur][i]);
			}
		}
		return count == numCourses;
	}
};