哈希集合(unordered_set)

哈希集合可以用来存储不重复的元素，利用哈希表快速搜索的特性，可以使得查找重复元素的速度比较快。

例题

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果 可以变为 1，那么这个数就是快乐数。

如果 n 是快乐数就返回 True ；不是，则返回 False 。

示例：

1
2
3
4
5
6
7
输入：19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

思路

首先，这些数肯定可以被分为快乐数和非快乐数。对于快乐数，我们按照happy算法，不断重复，最后一定可以得到1。对于非快乐数，我们只知道他始终无法变到1，无法确定其变化规律。但是，我们可以看到，一个四位的数，按照上面的算法，他最大能得到 $ 9^2+9^2+9^2+9^2 = 324 $, 可以看到会从四位数退化到三位数，同理，高于四位的数字也会随着算法进行退化到三位。而三位数最大能够到$ 9^2+9^2+9^2 = 243 $, 这意味着，所有的非快乐数，最终都会退化到[2, 243]之间，并且，对于每个数字其通过算法得到的结果是唯一的，所以，所有的非快乐数，都一定会得到[2, 243]之间的一个唯一的循环。

那么，我们就可以使用哈希集合来找出这个循环。

算法实现

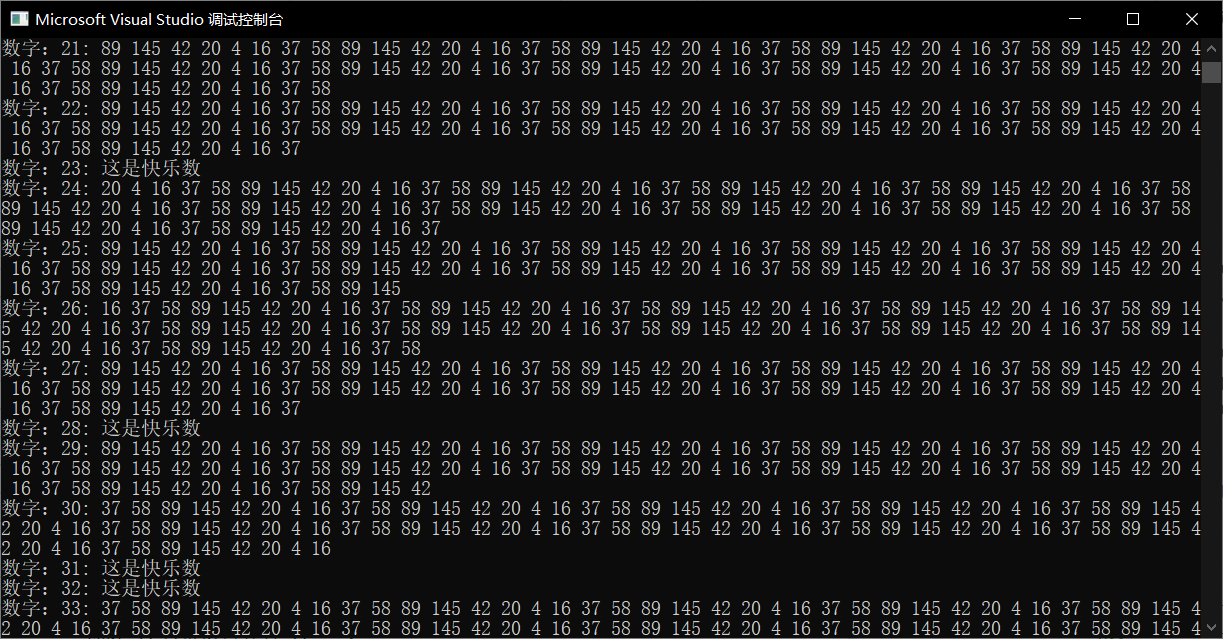
在这里，我计算了1-100的数，对这里面的非快乐数，调用happy算法100次，找到了这个循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <unordered_set>
#include<vector>

using namespace std;

int happy(int n) {
	int value = 0;
	while (n) {
		value += pow(n % 10, 2);
		n /= 10;
	}
	return value;
}

int main() {
	unordered_set<int> hashSet;
	int test[100];
	vector<int> repeat[100];
	for (int i = 0; i < 100; ++i)
		test[i] = i + 1;
	for (int i = 0; i < 100; ++i) {
		int num = test[i];
		int count = 1;
		hashSet.clear();
		while (1) {
			int next = happy(num);
			if (next == 1) break;
			else {
				if (hashSet.count(next) > 0) 
					repeat[i].push_back(next);
				else hashSet.insert(next);
			}
			num = next;
			if (count >= 100) break;
			count++;
		}
	}
	for (int i = 0; i < 100; ++i) {
		cout << "数字：" << i + 1 << ": ";
		if (!repeat[i].size())
			cout << "这是快乐数";
		for (int j = 0; j < repeat[i].size(); ++j) 
			cout << repeat[i][j] << " ";
		cout << endl;
	}

	return 0;
};

image1

可以看到，这个循环为4—>16—>37—>58—>89—>145—>42—>20—>4

找到这个循环以后，实现判断是否为快乐数，就非常简单了，不断调用happy算法，如果结果出现4，说明进入了这个循环，为非快乐数；反之则一定会出现1，为快乐数。

哈希映射

哈希映射最常见的应用就是移动窗口。比如在遍历一个数组时，使用左右两个指针，这两个指针就代表着这个窗口的左右边界，我们按照一定的规则依次移动两个指针，使得窗口不断滑动并记录窗口的状态，最终找出符合要求的窗口。但是，使用指针实现滑动窗口往往会比较麻烦且低效，而哈希表却相对更加高效。

例题

替换后的最长重复字符
给你一个仅由大写英文字母组成的字符串，你可以将任意位置上的字符替换成另外的字符，总共可最多替换 k 次。在执行上述操作后，找到包含重复字母的最长子串的长度。

注意:

注意:
字符串长度 和 k 不会超过 104。字符串长度 和 k 不会超过 104。

示例 1:

输入:
s = "ABAB", k = 2
输出:
4

解释:
用两个'A'替换为两个'B',反之亦然。

示例 2:

输入:
s = "AABABBA", k = 1
输出:
4

解释:
将中间的一个'A'替换为'B',字符串变为 "AABBBBA"。
子串 "BBBB" 有最长重复字母, 答案为 4。

思路

对于这个字符串s，我们使用一个滑动窗口于上面，left表示左边界，right表示有边界。如果滑动窗口内的子字符串满足题目的要求，那么这个字符串的长度就为right-left+1。

所以，问题的关键就成了判断一个窗口内的字符串内容是否满足要求。因为可以随便替换字符串里的内容，只对替换次数有要求，那么为了能找到尽可能长的这样的字符串，那么我们只需要找出这段字符串中，出现次数最多的字符，然后将其他的字符替换就好了，替换次数就可以表示为字符串长度-出现次数最多的字符的次数。于是，只要算出来的替换次数小于k，那么这就是个合法字符串，即此窗口是满足条件的。

最后，我们让right=0、left=0，如果窗口满足条件，就一直右移right，直到right移动到最右边时结束；当窗口不满足条件，就右移left；于是，最终的答案就为这些满足条件的窗口中最长的那个。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
	int characterReplacement(string s, int k) {
		int size = s.length();
		if(!size) return 0;
		if(k >= size) return size;
		int left = 0, right = 0, ans = 0, num = 0;
		char c;
		unordered_map<char, int> map;
		while(right <size){
			if(map.count(s[right]) <= 0) map.insert({s[right], 1});
			else ++map[s[right]];
			c = primChar(map);
			num = right-left+1-map[c];
			if(num > k){
				--map[s[left]];
				if(!map[s[left]]) map.erase(s[left]);
				++left;
			}else ans = max(ans, right-left+1);
			right++;
		}
		return ans;
	}
	char primChar(unordered_map<char, int> map){
		int max = 0;
		char c;
		for(auto i=map.begin(); i!=map.end(); ++i){
			if(i->second > max){
				max = i->second;
				c = i->first;
			}
		}
		return c;
	}
};

代码改进

上面的算法虽然是能够得到正确结果的，但是，其时间复杂度和空间复杂度都行，可以做出许多改进。

首先，我们在每次移动right后，都要重新判断窗口内出现次数最多的字符，但是实际上，如果移动right后，新加入的字符为原本就出现次数最多的字符，那么我们就完全没必要再判断了，直接继续移动right即可。

其次，当我们移动right后，发现新的窗口不满足条件，那么我们就得移动left了。最初采取的措施是每次移动left后，也都要重新判断窗口内出现次数最多的字符，但是实际上，如果移动left后，丢弃的那个字符不为原窗口出现次数最多的字符，那么我们也完全没必要判断了，直接继续移动right即可。

更高效的代码

上面虽然提出了改进的方法，但是整个算法仍旧不够简洁、高效。

因为我们需要找出的是满足条件的最长的子序列，其本质就是找出一个子序列中，存在最多的重复的字符，并且这个子序列满足条件。所以，其实我们的滑动窗口可以是一个只能变大的窗口，当出现更大的重复字符的数量时，才会使窗口变大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
	int characterReplacement(string s, int k) {
		int size = s.length();
		if(!size) return 0;
		if(k >= size) return size;
		int left = 0, right = 0, ans = 0, repeatNum= 0;
		unordered_map<char, int> map;//表中记录各元素出现的次数
		while(right <size){
			++map[s[right]];
			repeatNum = max(repeatNum, map[s[right]]);//最多的重复字符的数量
			if(right-left+1-repeatNum > k){//主要关心窗口长度
				--map[s[left]];
				++left;
			}
			ans = max(ans, right-left+1);
		    ++right;
		}
		return ans;
	}
};