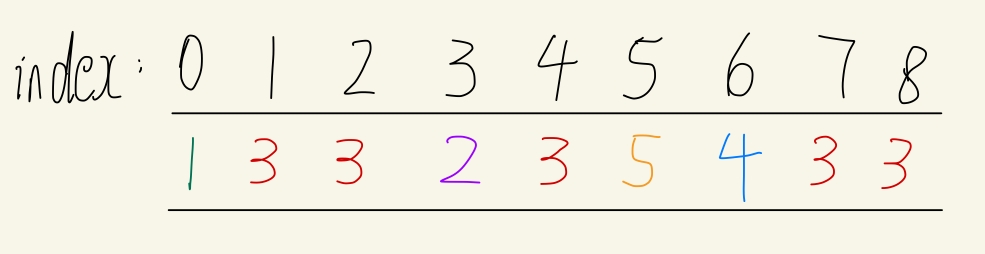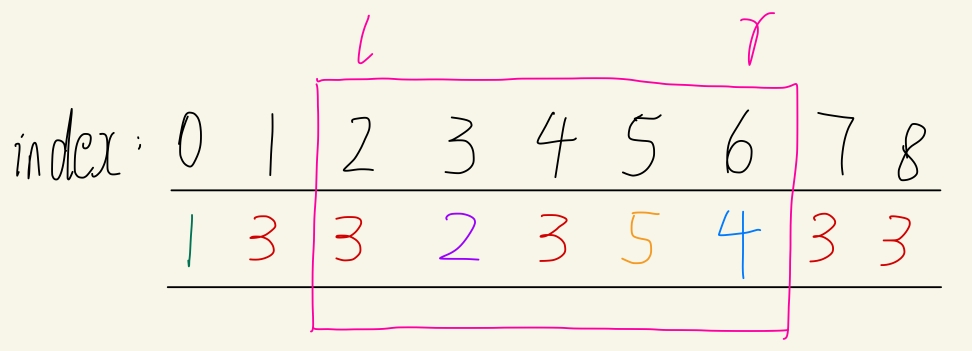题目描述

给出一些不同颜色的盒子，盒子的颜色由数字表示，即不同的数字表示不同的颜色。
你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 k*k 个积分。
当你将所有盒子都去掉之后，求你能获得的最大积分和。

示例：

输入：boxes = [1,3,2,2,2,3,4,3,1]
输出：23
解释：
[1, 3, 2, 2, 2, 3, 4, 3, 1]
----> [1, 3, 3, 4, 3, 1] (3*3=9 分)
----> [1, 3, 3, 3, 1] (1*1=1 分)
----> [1, 1] (3*3=9 分)
----> [] (2*2=4 分)

提示：

1 <= boxes.length <= 100
1 <= boxes[i] <= 100

思路

看见这种按照一定的规则求出给定数组的值，并且无法直接算出这个值的时候，就需要把这个给定数组拆分，然后求拆分后的子数组的值。于是自然而然就想到了动态规划。

最初想的是使用dp[l][r]数组来存放消除boxes里第l-r的盒子能获得的最大积分，但是这存在一个问题。比如当boxes为[2,3,2]时，dp[0][2]的最大值很明显应该为1+4=5（即先消除3，然后消除两个2）。若将问题拆分，dp[0][2]无非是使用dp[0][0]、dp[1][1]、dp[2][2]、dp[0][1]、dp[1][2]表示出来，但是遗憾的是，dp[0][2]没有办法用子数组的值表示出来，因为消除3以后，会导致两个2连接在一起，而子问题却是分成了dp[0][0]、dp[2][2]两个部分。

所以，使用dp[l][r][k]来表示消除boxes里第l-r的盒子以及boxes[r]右边的k个和boxes[r]相同颜色的盒子能够得到的最大积分。boxes[r]右边的那k个盒子最初不一定是相邻的，但是我们可以假设通过一定的操作将阻隔在中间的盒子先消除了。
假设我们有一个boxes为

images

那么dp[2][6][0]即为

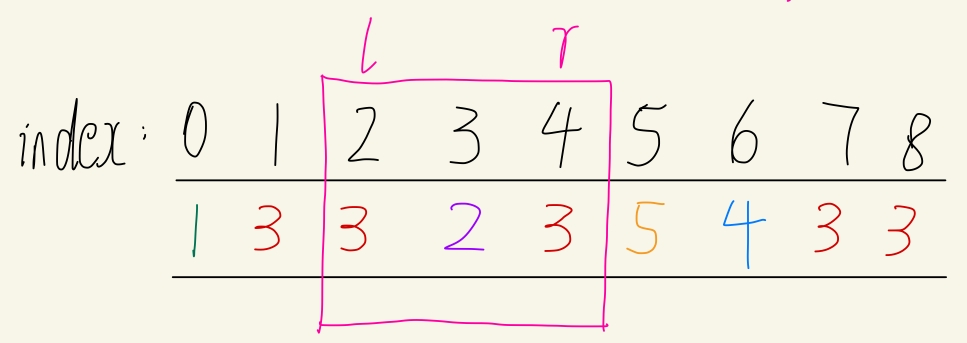
images

dp[2][4][2]为

images

而我们最终要求的其实就是dp[0][8][0]。
于是我们就可以对这样的问题拆成3部分，依旧是上面的boxes，我们就可以有如下几种操作：

  1. 我们直接将最后一个3消除并获得1积分，
  2. 我们从r往前面搜索，找到boxes[7]和boxes[8]相等且相邻都为3（很容易想到,两个一起消除得到的积分肯定更高。所以当在往前面搜索时，找到了与boxes[r]相等且相邻的，那么dp[l][r][k]就等于dp[l][--r][--k]），那么将这两个3一起消除并获得4积分，
  3. 我们继续往前面搜索，发现boxes[4]和boxes[8]、boxes[7]相等为3，那么我们将这三个3放一起，
  4. 继续搜索，
  5. 再继续，，此时已经找出了boxes中所有的3。
    而最终dp[0][8][0]就是上面这些情况的最大值。

所以，我们得到的动态规划的转移方程可以表示为：

images

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
	int dp[100][100][100] = {0};
    int removeBoxes(vector<int>& boxes) {
		return f(boxes, 0, boxes.size()-1, 0);
	}
	int f(vector<int>& boxes, int l, int r, int k) {
		if(l > r) return 0;
		if(dp[l][r][k]) return dp[l][r][k];
		while(l < r && boxes[r] == boxes[r-1]){//相邻且相等时,注意l小于r
			--r; ++k;
		}
		dp[l][r][k] = f(boxes, l, r-1, 0) + pow(k+1, 2);
		for(int i=l; i<r; ++i){//不相邻但相等时
			if(boxes[i] == boxes[r])
				dp[l][r][k] = max(dp[l][r][k], f(boxes, l, i, k+1)+f(boxes, i+1, r-1, 0) );
		}
		return dp[l][r][k];
	}
};