8-30最短路径算法总结

所谓最短路径问题是指：如果从图中某一顶点（源点）到达另一顶点（终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边的权值总和（称为路径长度）达到最小。

以下总结三种最短路径算法（c++）

Dijkstra算法

dijkstra算法只能用于边的权值都为正数的图，且只可算出起始节点到其他节点的最短路径（即单源最短路径）

算法描述：

使用三个辅助数组，数组S存储顶点是否被访问过，数组D存储当前的最短路径长度，数组Path存储节点的最短路径上的前驱节点。

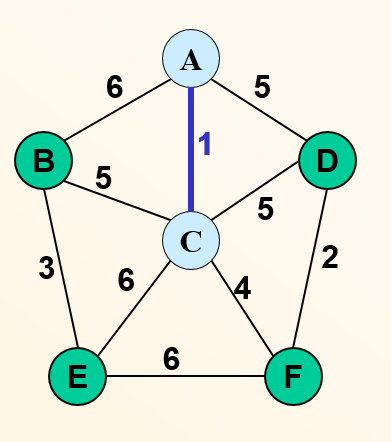
以这样一个无向图来举例：

images1

1.我们假定从节点V1出发，对这些数组进行初始化，此时V1是已经访问过的了，所以S[1]=true，能够与节点V1直接相连的，比如节点v2、V4，所以D[2]=5,D[4]=2，Path[2]=1,Path[4]=1;；而对于不能与节点V1直接相连的，距离就为无穷大，前驱节点初始为-1，比如D[3]=∞,Path[3]=-1。

所以初始时，我们就应该得到这样的三个数组：

images2

2.接着，我们从还未被访问过的节点中，选出与节点V1距离最短的节点，在这里就应该是节点V4，将这个节点设置为已访问（即S[4]=true），然后就可以根据与节点V4直接相连的节点之间的距离，更新数组D和数组Path了。

更新的规则是这样的：
假定存在一个与节点V4直接相连的节点Vj，节点vj到节点V4的距离为m，如果D[j] <= D[4]+m，那么D[j]和Path[j]不改变；如果D[j] > D[4]+m，那么D[j] = D[4]+m,Path[j] = 4

3.重复操作2，直到所有节点都被访问过。操作过程中，三个辅助数组变化如下：

images3

代码实现:

void Dijkstra(int node) {
	for (int i = 1; i < 7; ++i) {//初始化三个辅助数组
 		if (i != node)
			S[i] = false;
		D[i] = dic[node][i];
		if (dic[node][i] != INF)
			Path[i] = node;
		else Path[i] = -1;
	}
	Path[node] = -1;
	S[node] = true;
	
	for (int i = 0; i < 5; ++i) {//一共6个节点，所以只需要再循环5次
		int min = INF;
		int minNode;
		for (int j = 1; j < 7; ++j) {//找出距离最小的节点
			if (!S[j] && D[j] < min) {
				min = D[j];
				minNode = j;
			}
		}
		S[minNode] = true;//设置此节点已被访问
		for (int k = 1; k < 7; ++k) {//更新数组D、数组Path
			if (dic[minNode][k] + min < D[k]) {
				D[k] = dic[minNode][k] + min;
				Path[k] = minNode;
			}
		}
	}
	return;
}

代码测试:

#include <iostream>
#define INF 100000
using namespace std;

int dic[7][7];
bool S[7];
int D[7];
int Path[7];

void printPath() {
	for (int i = 1; i < 7; ++i) {
		cout << "V" << i;
		int t = i;
		while (Path[t] != -1) {
			cout << " -> V" << t;
			t = Path[t];
		}
		cout << " = " << D[i] << endl;
	}
}

void joinEdge(int i, int j, int edge) {
	dic[i][j] = edge;
	dic[j][i] = edge;
	return;
}

int main() {
	for (int i = 0; i < 7; ++i) {
		for (int j = 0; j < 7; ++j) {
			if (i == j) dic[i][j] = 0;
			else dic[i][j] = INF;
		}
 	}
	joinEdge(1, 2, 5);
	joinEdge(1, 4, 2);
	joinEdge(2, 4, 1);
	joinEdge(2, 3, 10);
	joinEdge(2, 5, 6);
	joinEdge(3, 6, 2);
	joinEdge(4, 5, 3);
	joinEdge(5, 6, 2);

	Dijkstra(1);
	cout << "D: " << endl;
	for (int i = 1; i < 7; ++i) {
		cout << "D[" << i << "]:" << D[i] << "  ";
	}
	cout << endl << "Path:" << endl;
	for (int i = 1; i < 7; ++i) {
		cout << "Path[" << i << "]:" << Path[i] << "  ";
	}
	cout << endl << "Path:" << endl;
	printPath();
	system("pause");
	return 0;
};

images4

Floyd算法

floyd算法可以用于有负权的图中，即使有负环，算法也可以检测出来,可以求任意点的最短路径，有向图和无向图的最小环和最大环。

算法描述:

images1

依然使用刚刚的图为例。使用一个二维数组D，存储两个节点之间的最短路径距离。从第一个节点开始，循环节点的个数那么多次，每次循环，都对数组D进行更新。那么初始时，数组D应该为：

images5

更新规则为：
假如正在进行k次更新，那么范围内的任意i、j如果满足D[i][j] > D[i][k]+D[k][j]，那么D[i][j] = D[i][k]+D[k][j]。

所以数组S的更新应该为如下：
images6

代码实现：

void Floyd() {
	for (int k = 1; k < 6; ++k) {
		for (int i = 1; i < 7; ++i) {
			for (int j = 1; j < 7; ++j) {
				if (D[i][k] + D[k][j] < D[i][j]) {
					D[i][j] = D[i][k] + D[k][j];
					D[j][i] = D[i][j];//无向图，更新时需要更新正反两面
				}
			}
		}
	}
}

代码测试：

#include <iostream>
#define INF 100000
using namespace std;

int D[7][7];

int main() {
	for (int i = 0; i < 7; ++i) {
		for (int j = 0; j < 7; ++j) {
			if (i == j) D[i][j] = 0;
			else D[i][j] = INF;
		}
 	}
	joinEdge(1, 2, 5);
	joinEdge(1, 4, 2);
	joinEdge(2, 4, 1);
	joinEdge(2, 3, 10);
	joinEdge(2, 5, 6);
	joinEdge(3, 6, 2);
	joinEdge(4, 5, 3);
	joinEdge(5, 6, 2);

	Floyd();
	for (int i = 1; i < 7; i++) {
		for (int j = 1; j < 7; ++j) {
			cout.width(7);
			cout << D[i][j] << " ";
		}
		cout << endl;
	}
	system("pause");
	return 0;
};