常见网格数据结构
学习《Polygon Mesh Processing》的第二章——Mesh Data Structure后,对其内容做一个学习总结。
大多数算法经常使用的操作的最小集:
① 访问每个顶点、边和面,包括以无序枚举这些元素;
② 按一定的方向遍历访问一个面的所有边,比如在一个面中查询前(后)一条边,
比如,通过对点的这些访问,可以渲染出相关的整个面;
③ 访问边的关联面,对于流形网格,根据方向的不同,可以访问左面或者右面。这
样就可以访问到邻面了;
④ 访问一条边的两个端点;
⑤ 至少可以访问一个给定顶点的一个关联面或者一个关联边。此外,对于流形网
格,可以枚举出一个顶点的单环领域内的所有其它元素。(即所有的关联面、关联边和临近的顶点)
1. 基于面的数据结构(Face-Based Data Structure)
· Face Set
这是一种最简单直观的用于表示曲面的数据结构,将一个曲面用许多足够小的三角形来近似表达,那么需要存储的,就是每个三角形的三个顶点的坐标。如果每个点的一个方向的坐标,使用32位单精度的数字来表示,则每个点使用12bytes来表示x、y、z轴方向坐标,而每个三角形需要存储3个顶点,即需要占据36bytes的存储空间。此外,根据Euler公式(曲面中面的数目约等于点的数目的两倍),那么平均算下来,这种数据结构消耗72bytes/顶点。
这种表示方式的特点:
① 简单直观;
② 无法显式获取连通信息;
③ 冗余;(对于不同面的公共点、公共面,需要重复地表示多次)
④ 常用于stereolithography(STL)文件中。
· Shared Vertex(Indexed Face Set)
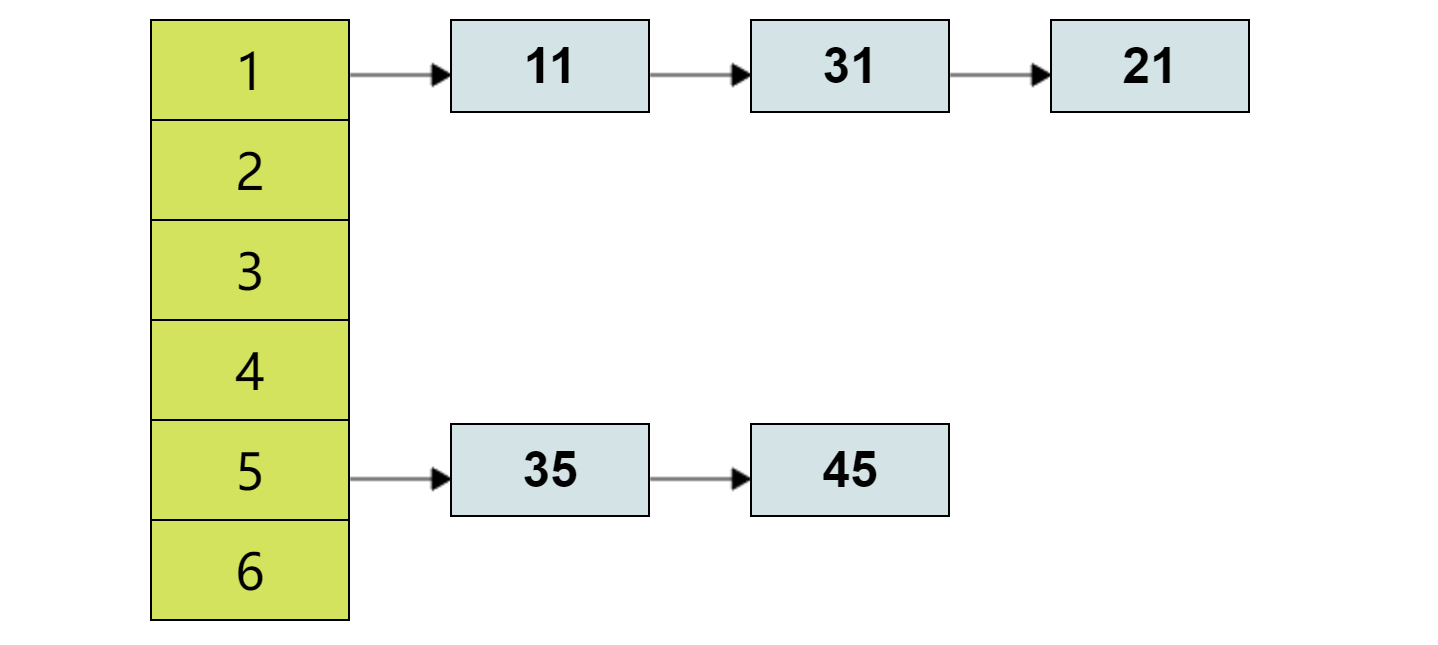
争对Face Set方式的冗余做出改进后,则得到了Shared Vertex数据结构。在这种数据结构中,依旧要对每个三角形进行存储,但不同之处在于,此方法使用一个表存储曲面涉及的所有顶点的坐标,故可以不直接存储三角形的每个顶点,而是存储点在表中对应的索引。
这种表示方式的特点:
① 消除了Face Set的冗余,更加节省存储空间;
② 能表示出连通信息,但如果没有额外的连通信息,这种数据结构需要付出高昂的搜索代价来恢复一个顶点的局部近邻信息,故对于大多数算法来说,这种数据结构是不够高效的;(比如查询两顶点是否相连的时间复杂度为O(F));
③ 在许多格式的文件中都有使用,比如OFF、OBJ和VRML。
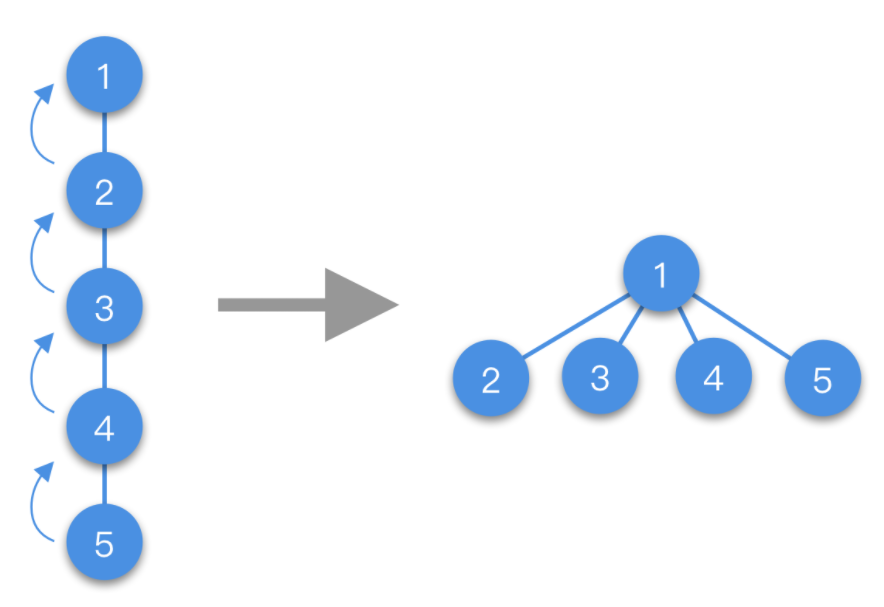
一种标准的基于面的三角网格数据结构中(如上图),每个面存储三个顶点以及和它相关的三个相邻三角形的引用。每个顶点除了自己的坐标外,还存储和它相邻的一个三角形的引用。基于这些连通信息,就可以通过绕着一个顶点循环枚举出它的单环领域,并实现上面提及的所有的频繁操作。其平均存储空间占用为 24bytes/面 + 16bytes/顶点 = 64bytes/顶点。
2. 基于边的数据结构(Edge-Based Data Structure)
最著名的基于边的数据结构主要有翼边winged-edge[Baumgart 72]和四方边quad-edge[Guibas and Stolfi 85]。
翼边数据结构如上图所示,每条边分别存储其两个端点、两个关联面以及左右关联面内的下一条和上一条边的引用。每个顶点和面存储各自关联的一条边。所以,算下来,这种数据结构总共占用的内存为16bytes/顶点 + 32bytes/边 + 4bytes/面 = 120bytes/顶点。(由Euler公式得 F ≈ 2V,E ≈ 3V)
虽然基于边的数据结构已经可以表示任意多边形网格,但是由于边不具有方向,在进行单环遍历时,需要做区分。(无法区分作为中心顶点的是边的第一个顶点还是第二个顶点)
3. 基于半边的数据结构(Halfedge-Based Data Structure)
基于半边的数据结构[Mantyla 88,Kettner 99],该结构通过将每个无方向的边分割成两个有方向的半边,从而避免了基于边的数据结构的单环遍历区分问题。
基于半边的数据结构如上图所示,半边沿每个面和每个边界以一致的逆时针顺序排列。因此,每个边界都可以看作一个空白面。此外,每个半边指定了一个唯一角(一个面中独占的顶点),所以如纹理坐标或者法线等信息可以存储在每个唯一角中。
对于每个半边,需要存储的对象的引用:
① 半边指向的顶点;
② 半边相邻面(如果是边界半边,则是一个nullptr);
③ 半边所在面或边界的下一条半边(逆时针方向);
④ 半边所在面或边界的上一条半边;
⑤ 半边对应的逆半边。
注意,如果两个对边总是成对地分组并存储在数组位置halfedges[i]和halfedges[i+1]中,则不需要存储逆半边。(在一个面中成对地存储了面中的一个半边和其对应的逆半边,那么在该逆半边所在的面中,就不再需要存储该逆半边了)此外,将两条半边组成一对,我们就得到了一个完整边的表示,这在当我们想要将数据与边关联,而不是与半边关联时是很重要。并且在一个面中的上一条半边的引用也可以省略,因为这可以通过步进下一个半边引用得到(即查找下一条半边的下一条半边)
对于每个面:存储它的一个半边的引用;
对于每个顶点:存储其外射的半边的引用;
由Euler公式可知,顶点的数目大约是边数目的3倍,那么顶点的数目大约是半边的数目的6倍,所以基于半边的数据结构的存储消耗大约为 16bytes/顶点 + 20bytes/半边 + 4bytes/面 = 144bytes/顶点。
半边数据结构使我们能够高效地枚举每个元素(即顶点,边,半边或面)的所有相邻元素。比如下图展示了列举给定顶点的单环领域。
从中心顶点出发,可以通过从中心顶点的外射半边开始(左),然后找到对应逆半边(中)和逆半边的下一条半边(右),并以此循环,不断按顺时针列举。
4. 有向边的数据结构(Directed-Edge Data Structure)
有向边数据结构[Campagna et al.98]是专门为三角形网格设计的一种半边数据结构的节省内存的变体。它基于引用网格中的每个元素(顶点,面以及半边)的索引。索引之间遵循着某些规则,这些规则隐秘地编码着三角形网格的一些连通信息。不像前面提及的将对半边组成对,这里则是将一个公共三角形的三个半边组合在一起。
如果
如果
定向边可以表示所有可以用通用半边数据结构表示的三角形网格。但是请注意,边界是由特殊的(如负数)索引处理的,该索引表示对边是无效的。遍历边界循环的开销更大,因为没有枚举下一个边界边的原子操作。对于通用的半边结构,它可以被沿边界的下一条半边有效地访问。
定向边的主要优点是它的高存储效率,但它无法处理混合了三角形和四边形的网格并且缺乏边的显式表示。(需要由半边间接得到)