PyTorch学习(1)——张量
参考:
PyTorch中文文档
PyTorch 学习笔记汇总
1 张量Tensor的结构在 PyTorch 0.4.0 之后,Tensor包含以下属性:
data:Tensor的值;
grad:data 的梯度;
grad_fn:创建 Tensor 所使用的 Function,是自动求导的关键,因为根据所记录的函数才能计算出导数;
requires_grad:是否需要梯度,并不是所有的张量都需要计算梯度;
is_leaf:是否叶子节点(张量),叶子节点的概念在计算图中会用到;
dtype:张量的数据类型,如 torch.FloatTensor,torch.cuda.FloatTensor;
shape:张量的形状(各维度的长度);
device:张量所在设备(CPU/GPU),可以进行切换。
2 Tensor的使用创建· 直接创建 torch.tensor1torch.tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False)
dtype:数据类型,默认与data一致;
pin_memo ...
常见网格数据结构
学习《Polygon Mesh Processing》的第二章——Mesh Data Structure后,对其内容做一个学习总结。
大多数算法经常使用的操作的最小集:
① 访问每个顶点、边和面,包括以无序枚举这些元素;
② 按一定的方向遍历访问一个面的所有边,比如在一个面中查询前(后)一条边,
比如,通过对点的这些访问,可以渲染出相关的整个面;
③ 访问边的关联面,对于流形网格,根据方向的不同,可以访问左面或者右面。这
样就可以访问到邻面了;
④ 访问一条边的两个端点;
⑤ 至少可以访问一个给定顶点的一个关联面或者一个关联边。此外,对于流形网
格,可以枚举出一个顶点的单环领域内的所有其它元素。(即所有的关联面、关联边和临近的顶点)
1. 基于面的数据结构(Face-Based Data Structure)· Face Set这是一种最简单直观的用于表示曲面的数据结构,将一个曲面用许多足够小的三角形来近似表达,那么需要存储的,就是每个三角形的三个顶点的坐标。如果每个点的一个方向的坐标,使用32位单精度的数字来表示,则每个点使用12bytes来表示x、y、z轴方向坐标,而每个三角形需要 ...
三维重建之图形变换
依旧是对鲁鹏老师的计算机视觉之三维重建课程 进行整理,在加上一些自己的理解。
在进行三维重建时,使用的都是齐次坐标(为什么要用齐次坐标?),故这里的变换都是针对图形的齐次坐标。
2D平面中的变换· 等距变换等距变换是指变化前后,图形中任意两点之间的距离保持不变。用矩阵表示则为:
\left(\begin{matrix}
x' \\
y' \\
1
\end{matrix}\right) =
\left(\begin{matrix}
\sigma cos\theta & -sin\theta & x_0 \\
\sigma sin\theta & cos\theta & y_0 \\
0 & 0 & 1
\end{matrix}\right)
\left(\begin{matrix}
x \\
y \\
1
\end{matrix}\right)当上式中的 时,表示保向变换(即欧式变换,我们日常中最常见平面中的平移、旋转);当时,表示逆向变换(即镜像变换)。
保向变换(欧式变换)
保向变换主要对 ...
三维重建之摄像机模型
参照北京邮电大学的鲁鹏老师的 :计算机视觉之三维重建
1. 相机内参· 简单相机模型
在不考虑畸变、偏置和单位转换的情况下,上图即为一个简单的摄像机模型。使用相似三角形法,很容易推导出在像素平面上的投影可以表示为:
\left\{\begin{matrix}
x' = f\frac{x}{z} \\
y' = f\frac{y}{z}
\end{matrix}\right.但是,以上在像素平面上的坐标P’是以像素平面上的点为坐标原点的(相当于以图像中间的点为坐标原点),这不太方便。我们习惯上会愿意以图像的左下角为坐标原点,所以需要在上述坐标加上偏置、。此外,在真实世界中,使用的作为坐标的单位,但在像素平面上,却是使用作为单位,故还需要将上述坐标乘以转换系数、(注意,前面的偏置也是使用作为单位的)。所以,最终可以得到如下的转换式:
\left\{\begin{matrix}
x' = fk\frac{x}{z}+c_x = \alpha\frac{x}{z}+c_x\\
y' = fl\frac{y}{z}+c_y = \beta\frac{y}{z}+c_y
\end{m ...
9-7算法,最小生成树总结
常用的两种求最小生成树的算法是Prim算法和Kruskal算法,这里对个算法做一个总结。
Prim算法:只可以用于连通图,当图中存在不连通的点时,此算法不适用。Kruskal算法:可以用于非连通图,这种情况下求出来的是各个子连通图的最小生成树。
Prim算法算法描述Prim算法和Dijkstra算法很相似:1.初始化一个空集合和一个记录数组,并从一个顶点出发,将这个顶点加入集合中;2.然后寻找与这个顶点之间距离最近(权值最低)的且没有在集合中的点,将寻找到的点加入集合,并使用这个点的数据对记录数组进行更新;3.以新加入的点作为顶点重复步骤2,直到所有的顶点都在集合中。
不同之处在于,Dijstra算法中记录数组记录的是其余点到出发顶点的最短距离,而Prim算法中记录数组记录的是其余点到集合中任意点的最短距离
代码实现123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263#include <iost ...
9-1算法,使用动态规划(预测赢家、石子游戏)
预测赢家题目描述给定一个表示分数的非负整数数组。 玩家 1 从数组任意一端拿取一个分数,随后玩家 2 继续从剩余数组任意一端拿取分数,然后玩家 1 拿,…… 。每次一个玩家只能拿取一个分数,分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。
给定一个表示分数的数组,预测玩家1是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。
示例 1:
输入:[1, 5, 2]
输出:False
解释:一开始,玩家1可以从1和2中进行选择。
如果他选择 2(或者 1 ),那么玩家 2 可以从 1(或者 2 )和 5 中进行选择。如果玩家 2 选择了 5 ,那么玩家 1 则只剩下 1(或者 2 )可选。
所以,玩家 1 的最终分数为 1 + 2 = 3,而玩家 2 为 5 。
因此,玩家 1 永远不会成为赢家,返回 False 。
示例 2:
输入:[1, 5, 233, 7]
输出:True
解释:玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个,玩家 1 都可以选择 233 。
最终,玩家 ...
8-30最短路径算法总结
所谓最短路径问题是指:如果从图中某一顶点(源点)到达另一顶点(终点)的路径可能不止一条,如何找到一条路径使得沿此路径上各边的权值总和(称为路径长度)达到最小。
以下总结三种最短路径算法(c++)
Dijkstra算法
dijkstra算法只能用于边的权值都为正数的图,且只可算出起始节点到其他节点的最短路径(即单源最短路径)
算法描述:使用三个辅助数组,数组S存储顶点是否被访问过,数组D存储当前的最短路径长度,数组Path存储节点的最短路径上的前驱节点。
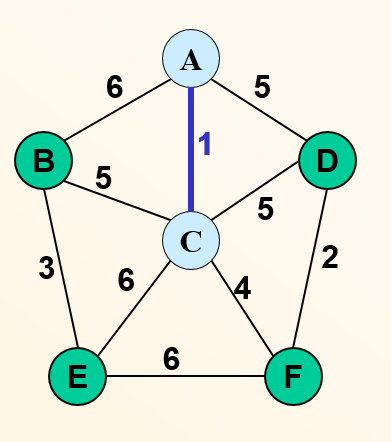
以这样一个无向图来举例:
1.我们假定从节点V1出发,对这些数组进行初始化,此时V1是已经访问过的了,所以S[1]=true,能够与节点V1直接相连的,比如节点v2、V4,所以D[2]=5,D[4]=2,Path[2]=1,Path[4]=1;;而对于不能与节点V1直接相连的,距离就为无穷大,前驱节点初始为-1,比如D[3]=∞,Path[3]=-1。
所以初始时,我们就应该得到这样的三个数组:
2.接着,我们从还未被访问过的节点中,选出与节点V1距离最短的节点,在这里就应该是节点V4,将这个节点设置为已访问(即S[4]=true ...
8-15算法,移除盒子(动态规划)
题目描述给出一些不同颜色的盒子,盒子的颜色由数字表示,即不同的数字表示不同的颜色。你将经过若干轮操作去去掉盒子,直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子(k >= 1),这样一轮之后你将得到 k*k 个积分。当你将所有盒子都去掉之后,求你能获得的最大积分和。
示例:
输入:boxes = [1,3,2,2,2,3,4,3,1]
输出:23
解释:
[1, 3, 2, 2, 2, 3, 4, 3, 1]
----> [1, 3, 3, 4, 3, 1] (3*3=9 分)
----> [1, 3, 3, 3, 1] (1*1=1 分)
----> [1, 1] (3*3=9 分)
----> [] (2*2=4 分)
提示:
1 <= boxes.length <= 1001 <= boxes[i] <= 100
思路看见这种按照一定的规则求出给定数组的值,并且无法直接算出这个值的时候,就需要把这个给定数组拆分,然后求拆分后的子数组的值。于是自然而然就想到了动态规划。
最初想的是使用dp[l][r ...
8-14 常用排序算法
对数据结构中非常重要的十大内部排序算法以及七大查找算法做一个总结排序算法可按照如下进行分类:
内部排序:指的是只用到了电脑内存而不使用外存的排序方式。
比较排序比较排序,顾名思义,即需要通过比较两个元素的大小关系来确定先后顺序。而在比较排序中,又可以分为交换、插入、选择和归并四类。
交换:根据比较结果交换两个元素。插入:将当前遍历到的元素插入到之前已经排好序的序列中。选择:不断选出当前剩余序列中最大(或最小)的元素出来。
交换1. 冒泡排序(Bubble Sort)冒泡排序是三大基础排序中的一种,比较简单,不再赘述,直接上代码。
1234567void BubbleSort(int* arr, int n) { for(int i=0; i<n; ++i) for(int j=0; j<n-i-1; ++j) { if(arr[j] > arr[j+1]) swap(arr[j], arr[j+1]); }}
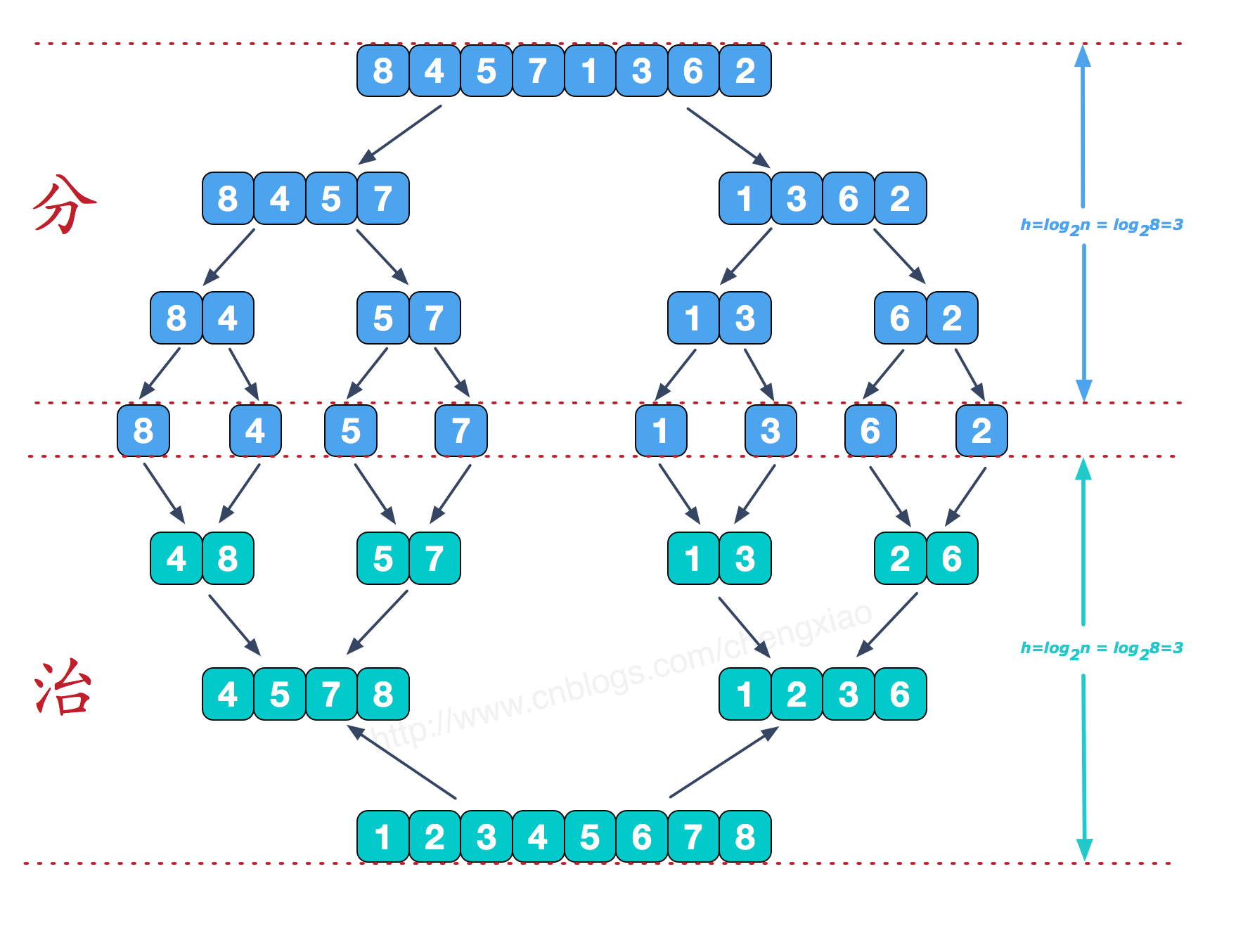
2. 快速排序(Quick Sort)快速排序是对冒泡排序的一种改进,使用了分治思想。
思想:通过一趟 ...
8-12算法,利用哈希表实现图的深拷贝
题目描述给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 ...