8-7算法,哈希集合、哈希映射的应用
哈希集合(unordered_set)哈希集合可以用来存储不重复的元素,利用哈希表快速搜索的特性,可以使得查找重复元素的速度比较快。
例题编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
示例:
1234567输入:19输出:true解释:12 + 92 = 8282 + 22 = 6862 + 82 = 10012 + 02 + 02 = 1
思路首先,这些数肯定可以被分为快乐数和非快乐数。对于快乐数,我们按照happy算法,不断重复,最后一定可以得到1。对于非快乐数,我们只知道他始终无法变到1,无法确定其变化规律。但是,我们可以看到,一个四位的数,按照上面的算法,他最大能得到 $ 9^2+9^2+9^2+9^2 = 324 $, 可以看到会从四位数退化到三位数,同理,高于四位的数字也会随着算法进行退化到三位。而三位数最大能够到 ...
8-7 哈希表(散列表)
简介哈希表是一种使用哈希函数组织数据的数据结构,它支持快速插入和搜索。
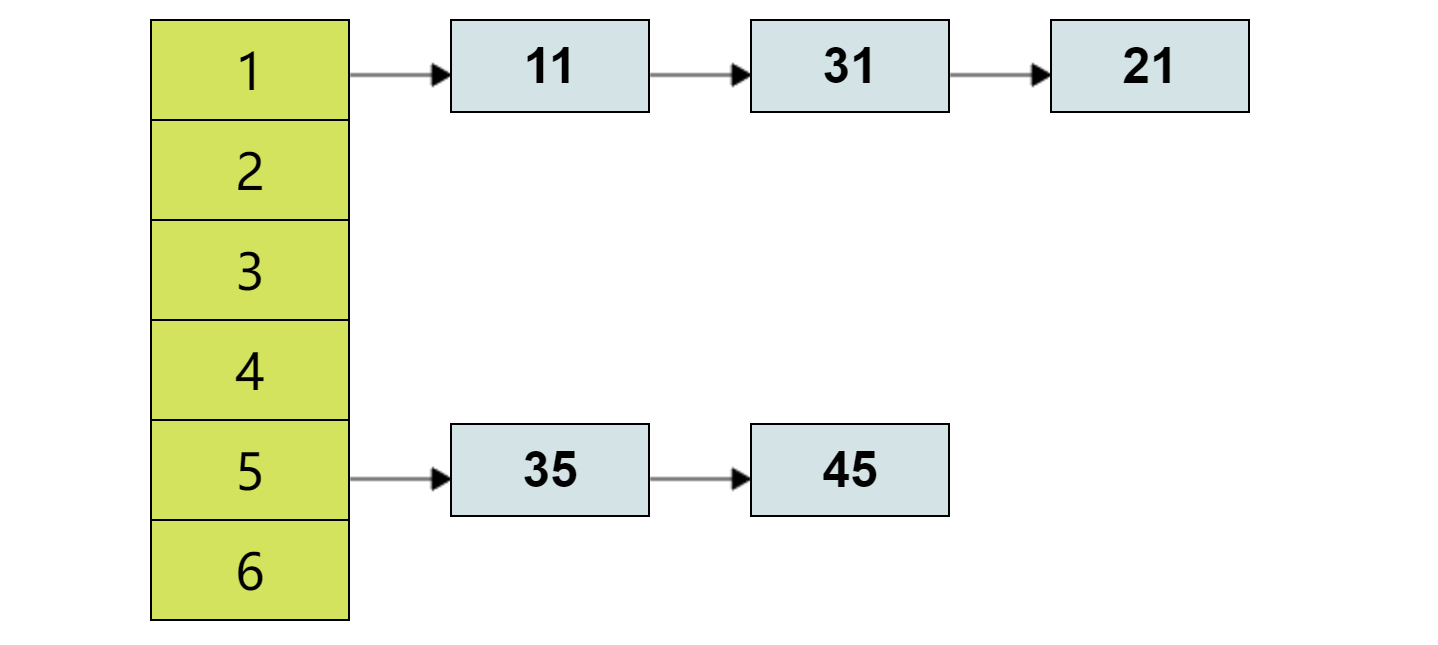
原理哈希表(又称散列表)的原理为:借助 哈希函数,将键映射到存储桶地址。更确切地说,
首先开辟一定长度的,具有连续物理地址的桶数组;
当我们插入一个新的键时,哈希函数将决定该键应该分配到哪个桶中,并将该键存储在相应的桶中;
当我们想要搜索一个键时,哈希表将使用哈希函数来找到对应的桶,并在该桶中进行搜索。
作者:力扣 (LeetCode)链接:https://leetcode-cn.com/leetbook/read/hash-table-plus/kd67i/
可以联想到cache的工作原理。
负载因子实际利用桶的个数与桶的总数 的比值,称为负载因子,反映了哈希表的装满程度。负载因子太低了,会使得大量存储空间被浪费,负载因子太高了,出现哈希冲突的概率就会难以接受。比较合理的负载因子是 0.7,如果数据量是 7,则会创建 10 个桶,以此类推。随着插入的数据量的增加,计算机会逐渐增加桶的个数,并选择合适的哈希函数,使得数据经过映射之后能均匀地分布在桶中。
哈希冲突不同的key被哈希函数映射到了同一个 ...
8-5算法,打家劫舍
打家劫舍题一共有三道,首先看看最简单的:
打家劫舍(一)题目描述你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷
窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
0 <= nums.length <= 1000 <= nums[i] <= 400
思路这是一道很明显的动态规划题,规定用数组dp来存储偷窃到的最高金额,数组nums ...
8-4,判断有向图是否有圈的两种常用方法
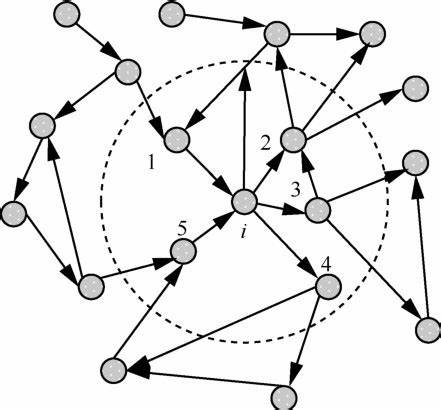
有向无环图(Directed Acycling Graph):是图中没有回路(环)的有向图。是一类具有代表性的图,主要用于研究工程项目的工序问题、工程时间进度问题等。
那么首先,讨论判断一个有向图是否有圈的算法,以及他的应用。
1. 拓扑排序算法描述:
对一个有向无圈图,首先找出所有的入度为0的点,访问、操作这些点;
删除所有的入度为0的点,以及所有的和这些点相连的边;
重复1、2步操作直到没有入度为0的点,对一个有向无圈图来说,最后一定会一个点都不剩了,否则,说明这个有向图是有圈的。
2. DFS算法描述:
规定,对以访问的点设1,正在访问的点设0,未访问的点设-1;
从任意点出发,对该点深度优先搜索,如果在搜索的过程中发现下一个点为0,出现了重复访问,说明有圈;
当所有的点都变成1,仍旧没有出现重复访问,说明没有圈。
3. 应用在选择课程的时候,有的课程必须要求有先修课程,那么将这些课程的关系抽象出来即是有向无圈图。例题可以参考上一篇文章:课程表(一)
在这里采用DFS重新实现该算法:
1234567891011121314151617181920212223242526272 ...
8-4算法,课程表(一)
题目描述你这个学期必须选修numCourse门课程,记为0到numCourse-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完 成课程 1。这是不可能的。
提示:
输入的先决条件是由 边缘列表 表示的图形,而不是 邻接矩阵 。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
1 <= numCourses <= 10^5
思路这道题实际上就是判断有向图是否存在圈(从一个节点开始,能够回到这个节点),那么在所有课程中,入度为0的课程,一定是其他课程的先修课程或者为单独的课程 ...
8-2算法,二叉树展开为链表
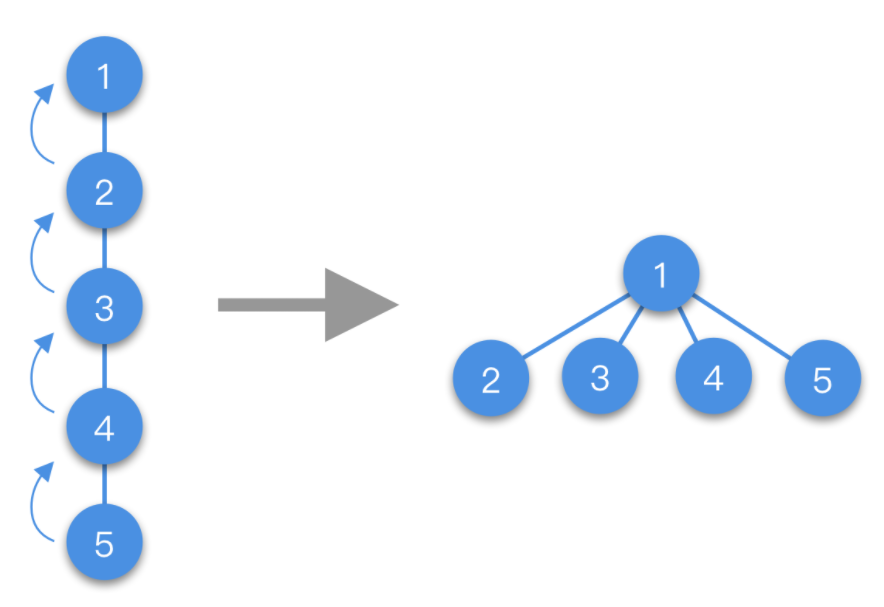
题目描述给定一个二叉树,原地将它展开为一个单链表。
树节点的定义为:
Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
例如,给定二叉树
1
/ \
2 5
/ \ \
3 4 6
将其展开为:
1
\
2
\
3
\
4
...
8-1算法,除法求值
题目描述给出方程式 A / B = k, 其中 A 和 B 均为用字符串表示的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
示例 :给定: a / b = 2.0, b / c = 3.0问题: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?返回: [6.0, 0.5, -1.0, 1.0, -1.0 ]
输入为:vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries(方程式,方程式结果,问题方程式), 其中 equations.size() == values.size(),即方程式的长度与方程式结果长度相等(程式与结果一一对应),并且结果值均为正数。以上为方程式的描述。 返回vector类型。
基于上述例子,输入如下:
equations(方程式) = ...
7-31算法,被围绕的区域(一)
题目描述给定一个二维的矩阵,包含 ‘X’ 和 ‘O’(字母 O)。
找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
思路此题可以使用并查集,首先进行遍历,将所有相邻的’O’归于一个集合里面,同时,将边界上的’O’与一个虚拟的节点归为一个集合以作区分。然后,再次遍历,将所有既是’O’又不和那个虚拟节点一个集合的元素改成’X’输出。
代码 ...
7-31 并查集
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
1. 并查集的主要操作
初始化把每个点所在集合初始化为其自身。通常来说,这个步骤在每次使用该数据结构时只需要执行一次,无论何种实现方式,时间复杂度均为O(N)。
查找查找元素所在的集合,即根节点。
合并将两个元素所在的集合合并为一个集合。通常来说,合并之前,应先判断两个元素是否属于同一集合,这可用上面的“查找”操作实现。
2. 并查集代码实现
1.初始化
12for(int i = 0; i < length(pre); i++) pre[i] = i;
2.查找
123456int unionSearch(int root) { root = pre[root];//找到root的直接上级 while(root != pre[root])//root的上级不是自己,即root不是根 root = pre[root]; return root;//找到根}
3.合并
123456void join(int x, int y ...
7-30算法:有效的括号
题目描述给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效字符串。
示例 1:输入: "()"
输出: true
示例 2:输入: "()[]{}"
输出: true
思路1,创建一个空栈,当字符串不为空时,从第一个字符开始遍历字符串,如果遇到’(‘、’[‘、’{‘,就将字符压入一个栈中;如果遇到’)’、’]’、’}’,则判断此时栈顶的元素是否是对应的前括号比如')'对应'(',如果满足对应关系,就将栈顶元素取出,继续遍历,如果不满足对应关系,则返回false。遍历完成后,如果栈不为空,返回false,反之返回true。
1234567891011121314151617import java.util.Stack;class Solution { public boolean isValid(String s) { ...